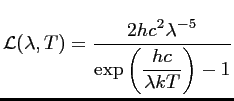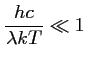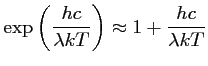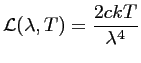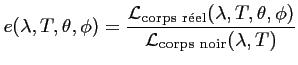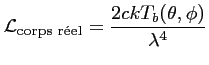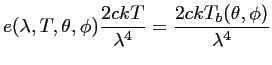Next: 1.2 Radiomètre à puissance
Up: 1. Télédétection de l'humidité
Previous: 1. Télédétection de l'humidité
Contenu
Dans le domaine des hyperfréquences, les instruments de télédétection peuvent être classés dans
deux grandes familles : celle des radars, instruments actifs, et celle des
radiomètres, instruments passifs. Ces instruments ont en commun qu'ils mesurent
le rayonnement électromagnétique, pour une longueur
d'onde donnée, provenant de cibles
éloignées. Le but est de déduire les caractéristiques
physiques des cibles observées, ici l'humidité ou la
salinité de surface, en choisissant au mieux le type
d'instrument et la longueur d'onde utilisée.
Onde électromagnétique, Longueur d'Onde, Domaine
micro-onde, Bande L
La lumière visible est une onde électromagnétique dont la
longueur d'onde est située dans la bande
visible
.
Chaque couleur que nous percevons indique une longueur
d'onde différente : les deux valeurs extrêmes que nous
pouvons distinguer sont 0.4
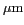 (violet) et 0.7
(violet) et 0.7
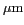 (rouge).
(rouge).
Le domaine des hyperfréquences, dit encore des
micro-ondes, s'étend dans des longueurs d'onde beaucoup
plus grandes. Ce domaine est lui même divisé en bande, la bande L
s'étendant entre 20 cm et 80 cm, soit, en fréquence, entre
0.390 GHz et 1.550 GHz.
Les radars sont des instruments actifs. Une onde
électromagnétique est envoyée par une antenne sur une cible
qui, suivant ses propriétés physiques, va plus ou
moins absorber ce rayonnement. Cette même antenne (ou une
antenne différente) est alors
utilisée pour mesurer la puissance du signal renvoyé et l'on
en déduit ainsi les caractéristiques de la cible. Lorsque la
cible est une surface naturelle, la puissance rétro-diffusée
est toutefois très sensible à la topographie de la surface
observée (rugosité du sol, de la végétation ou de la mer)
qui doit donc être prise en compte pour interpréter les mesures.
La seconde famille est celle des instruments passifs. Aucune
onde n'est envoyée, l'antenne d'un radiomètre ne
fonctionnant qu'en réception. Seule l'émission naturelle du
rayonnement par la surface est mesurée : cette émission
naturelle est caractérisée par une quantité appelée température de brillance ( ).
).
Corps noir et Température de Brillance
Un corps noir est un corps idéal absorbant toute l'énergie
électromagnétique qu'il reçoit : s'il n'est pas chauffé, il
n'émet aucun rayonnement, il est donc noir.
Lorsqu'il est chauffé, il rayonne pour contrebalancer
l'énergie qu'il reçoit et, tout comme la braise d'un
feu de cheminée, la longueur d'onde de ce rayonnement (sa
couleur ) change en fonction de la
température.
Dans un cas idéal, MAX PLANCK
a montré, en 1900, que l'énergie rayonnée par un corps
noir à une longueur d'onde donnée ne dépend que de sa
température.
L'énergie rayonnée par une surface quelconque, elle, ne
dépend pas que de sa température. La température de
brillance de cette surface est la température qu'aurait un
corps noir rayonnant la même énergie.
Comme il le sera précisé dans les paragraphes suivants, la
précision contraignante sur la mesure de l'humidité et de la
salinité, ainsi que les effets importants de la topographie
des surfaces observées, font que les radiomètres sont dans ce
cas préférés aux radars. D'autre part, l'utilisation de la
longueur d'onde
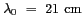 (fréquence
centrale
(fréquence
centrale
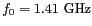 ), au sein de la bande L,
offre plusieurs avantages :
), au sein de la bande L,
offre plusieurs avantages :
- cette partie de la bande L est dite protégée c.-à-d. qu'il est (normalement)
interdit d'émettre (relais et téléphones portables, radars
d'aéroport...) autour de cette fréquence.
- l'atténuation du signal par la vapeur d'eau et
l'eau liquide, contenue notamment dans les nuages, est
quasi-nulle
- la température de brillance dépend
fortement de la présence d'eau à la surface du sol (3 à 5 cm
de profondeur contre seulement 1 cm à plus haute fréquence)
- la sensibilité radiométrique à la salinité de
surface est optimale.
Température de brillance
![$ T_b~[\textrm{K}]$](img5.gif) En 1900, MAX PLANCK établit grâce à une loi empirique la
variation de la luminance
En 1900, MAX PLANCK établit grâce à une loi empirique la
variation de la luminance
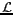 d'un corps noir en fonction de
sa température
d'un corps noir en fonction de
sa température 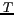 et de la longueur d'onde
et de la longueur d'onde 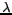 du
rayonnement émis Ulaby:
du
rayonnement émis Ulaby:
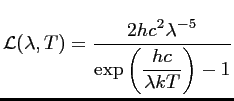 |
(1.1) |
où la luminance
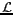 est une puissance par unité surface, par
stéradian et par longueur d'onde (
est une puissance par unité surface, par
stéradian et par longueur d'onde (
![$ [\textrm{W.m}^{-2}.\textrm{sr}^{-1}.\textrm{m}^{-1}]$](img10.gif) ),
), 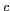 est la vitesse de
la lumière (
est la vitesse de
la lumière (
![$ [\textrm{m.s}^{-1}]$](img12.gif) ),
), 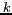 la constante de
BOLTZMANN et
la constante de
BOLTZMANN et 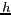 la constante de PLANCK
(
la constante de PLANCK
(
![$ [\textrm{J.s}]$](img15.gif) ).
).
Dans le domaine micro-onde, le rapport
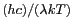 est de l'ordre de
est de l'ordre de
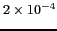 pour
pour
 et
et
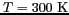 , l'approximation de Rayleigh-Jeans est alors
possible :
, l'approximation de Rayleigh-Jeans est alors
possible :
Alors que le rayonnement du corps noir est
isotrope (identique dans toutes les directions), celui d'un corps réel peut dépendre de la
direction d'observation
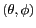 (coordonnées
sphériques traditionnelles). L'émissivité
(coordonnées
sphériques traditionnelles). L'émissivité
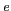 est
introduite pour faire le lien entre la luminance d'un corps
réel et celle du corps noir :
est
introduite pour faire le lien entre la luminance d'un corps
réel et celle du corps noir :
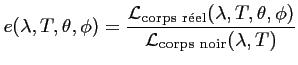 |
(1.4) |
La température de brillance
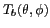 d'une
surface quelconque est la température
d'une
surface quelconque est la température 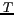 que devrait
avoir un corps noir pour que sa luminance soit semblable à celle
de ce corps réel.
que devrait
avoir un corps noir pour que sa luminance soit semblable à celle
de ce corps réel.
La température de brillance est donc telle que :
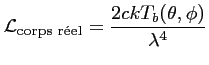 |
(1.5) |
Donc, d'après (1.3) :
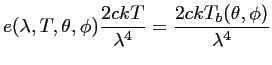 |
(1.6) |
Soit la relation entre la température de brillance et la
température physique, pour une longueur d'onde fixée:
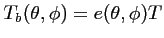 |
(1.7) |
avec
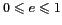 .
.
La température de brillance ( ) d'une surface continentale
dépend principalement de l'humidité de surface du sol
) d'une surface continentale
dépend principalement de l'humidité de surface du sol
 [
[
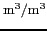 ], de l'épaisseur optique
de la couverture végétale
], de l'épaisseur optique
de la couverture végétale
![$ \tau~[\textrm{Nepers}]$](img34.gif) et de sa température de
surface
et de sa température de
surface
![$ T_s~[\textrm{K}]$](img35.gif) Wigneron1 Wigneron2. D'autres effets comme la
topographie, la rugosité du terrain, le type de sol ou encore
la nature de la couverture végétale sont aussi à
prendre en compte. Cependant, étant donné qu'ils sont
constants dans le temps, des données externes (modèles
numériques de terrain, données satellites...) peuvent être
utilisées pour corriger ces contributions.
Wigneron1 Wigneron2. D'autres effets comme la
topographie, la rugosité du terrain, le type de sol ou encore
la nature de la couverture végétale sont aussi à
prendre en compte. Cependant, étant donné qu'ils sont
constants dans le temps, des données externes (modèles
numériques de terrain, données satellites...) peuvent être
utilisées pour corriger ces contributions.
En bande L, le modèle de transfert radiatif du premier ordre dit modèle
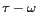 , où
, où 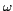 est l'albédo de la
végétation) relit indirectement les trois
paramètres physiques (
est l'albédo de la
végétation) relit indirectement les trois
paramètres physiques (
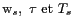 ) à
) à  .
La couverture végétale est le principal obstacle
entre l'instrument et le sol. Il est impératif de
disposer de mesures indépendantes de
.
La couverture végétale est le principal obstacle
entre l'instrument et le sol. Il est impératif de
disposer de mesures indépendantes de  pour des configurations
variées, en terme d'angles d'incidence, de polarisation ou
de fréquence pour pouvoir éliminer la contribution de la
canopée, la capacité de mesure multi-angulaire étant sans
doute la plus efficace Wigneron3. A cette
condition, l'humidité de surface des sols reste mesurable pour une
densité surfacique de la biomasse inférieure à
5 kg
pour des configurations
variées, en terme d'angles d'incidence, de polarisation ou
de fréquence pour pouvoir éliminer la contribution de la
canopée, la capacité de mesure multi-angulaire étant sans
doute la plus efficace Wigneron3. A cette
condition, l'humidité de surface des sols reste mesurable pour une
densité surfacique de la biomasse inférieure à
5 kg
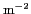 , ce qui représente 65
, ce qui représente 65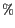 des terres
émergées Kerr1. Une fois l'humidité de surface
connue avec une précision suffisante, il est possible de
retrouver l'humidité du sol dans la zone vadose, la zone
dans laquelle la végétation va puiser une partie de son eau Calvet1.
des terres
émergées Kerr1. Une fois l'humidité de surface
connue avec une précision suffisante, il est possible de
retrouver l'humidité du sol dans la zone vadose, la zone
dans laquelle la végétation va puiser une partie de son eau Calvet1.

La salinité est définie comme le rapport entre la masse de
sel et la masse d'eau de mer, en gramme de sel par
kilogramme d'eau de mer :
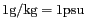 , pratical
salinity unit. Or, la situation est différente du cas de la mesure de
l'humidité. En effet, la salinité de l'eau de mer fait peu
varier la température de brillance des océans1.1. Même
si, là encore, la bande L semble la plus indiquée, le signal
reste faible. Cette donnée, combinée avec une
contrainte forte sur la précision de la mesure (0.1 psu),
conduit à faire de la modélisation du problème direct une
étape majeure dans le processus d'estimation de la salinité
de surface des océans (SSS pour Sea surface
Salinity) à partir des températures de brillance.
, pratical
salinity unit. Or, la situation est différente du cas de la mesure de
l'humidité. En effet, la salinité de l'eau de mer fait peu
varier la température de brillance des océans1.1. Même
si, là encore, la bande L semble la plus indiquée, le signal
reste faible. Cette donnée, combinée avec une
contrainte forte sur la précision de la mesure (0.1 psu),
conduit à faire de la modélisation du problème direct une
étape majeure dans le processus d'estimation de la salinité
de surface des océans (SSS pour Sea surface
Salinity) à partir des températures de brillance.
La température de brillance des océans va varier en fonction de 3
facteurs principaux : la salinité, bien sûr, mais aussi la
température de surface (SST pour Sea Surface
Temperature) et enfin la rugosité de la mer,
principalement liée à la vitesse du vent. Ainsi,
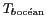 peut être
vu comme la somme de deux contributions :
peut être
vu comme la somme de deux contributions :
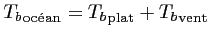 |
(1.8) |
La contribution principale
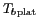 est celle d'une mer
sans vague, une mer idéale plate. La contribution secondaire
est celle d'une mer
sans vague, une mer idéale plate. La contribution secondaire
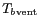 est celle de la rugosité de la mer :
la formation des vagues, de l'écume et de la houle induite
par le vent va apporter une correction non négligeable aux
valeurs obtenues par le modèle précédent.
est celle de la rugosité de la mer :
la formation des vagues, de l'écume et de la houle induite
par le vent va apporter une correction non négligeable aux
valeurs obtenues par le modèle précédent.
Même si le radiomètre possède une sensibilité de l'ordre du
Kelvin, ce qui, on le verra dans la section suivante,
représente une forte contrainte instrumentale, l'erreur sur
l'estimation de la SSS est alors de 2 psu. Or, la précision
doit être de l'ordre de 0.1 psu pour que la salinité soit
utilisable scientifiquement.
Afin d'atteindre ce seuil, des
mesures élémentaires indépendantes devront être moyennées. Il est donc important de
pouvoir obtenir le maximum de mesures indépendantes pour un même pixel au
cours d'un seul passage de l'instrument.
Ces mesures pourront aussi être moyennées spatialement,
sur des zones de 200 km  200 km, et
temporellement, sur 10 jours. Contrairement à ce qui se passe pour
l'humidité, ce n'est donc pas tant la résolution spatiale que
la stabilité et l'étalonnage de l'instrument qui devront
être le trait dominant du radiomètre, sans pour autant
négliger la sensibilité radiométrique.
200 km, et
temporellement, sur 10 jours. Contrairement à ce qui se passe pour
l'humidité, ce n'est donc pas tant la résolution spatiale que
la stabilité et l'étalonnage de l'instrument qui devront
être le trait dominant du radiomètre, sans pour autant
négliger la sensibilité radiométrique.
De même que pour l'humidité, des données de
SST et de vent (vitesse et direction) issues de mesures
satellites ou de sorties de modèles météorologiques
doivent être intégrées avec une précision suffisante afin de
pouvoir inverser la relation établie entre la température de
brillance et la salinité.




Next: 1.2 Radiomètre à puissance
Up: 1. Télédétection de l'humidité
Previous: 1. Télédétection de l'humidité
nous
2005-03-31