
D’après (A.3) et (A.4), on a repectivement

signifiant que les vecteurs 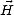 et
et 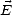 sont transversaux à
sont transversaux à 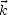 qui est la direction de propagation de l’onde
(voir l’annexe E) ; les vecteurs champs électrique et magnétique appartiennent au plan orthogonal au
vecteur
qui est la direction de propagation de l’onde
(voir l’annexe E) ; les vecteurs champs électrique et magnétique appartiennent au plan orthogonal au
vecteur 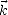 appelé plan de polarisation.
appelé plan de polarisation.
On va maintenant établir la relation entre 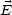 et
et 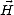 . On écrit le champ électrique d’après (A.8)
comme
. On écrit le champ électrique d’après (A.8)
comme
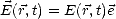 | (B.19) |
où E(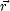 , t) est la norme du champ électrique et
, t) est la norme du champ électrique et 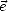 est le vecteur unitaire qui porte le champ électrique.
On sait désormais que
est le vecteur unitaire qui porte le champ électrique.
On sait désormais que 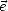 est dans le plan orthogonal à
est dans le plan orthogonal à 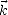 ; on va définir le trièdre orthogonal direct
(
; on va définir le trièdre orthogonal direct
(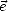 ,
, 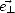 ,
, 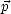 ), où
), où 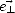 est dans le plan de polarisation et est orthogonal à
est dans le plan de polarisation et est orthogonal à 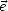 et où
et où 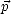 =
= 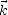 /|
/|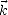 | est la direction de
propagation de l’onde. Dans ce repère, on a
| est la direction de
propagation de l’onde. Dans ce repère, on a
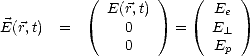
et
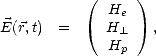
où l’on cherche à déterminer He, H et Hp, qui sont les composantes de
et Hp, qui sont les composantes de 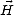 respectivement le long de
respectivement le long de 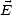 , orthogonalement à
, orthogonalement à 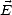 dans le plan de polarisation et le long de
dans le plan de polarisation et le long de
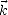 1 en
fonction de Ee .
1 en
fonction de Ee .
D’après (A.2), on a
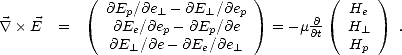
En utilisant (B) et (A.12), on obtient
d’où l’on déduit que 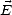 et
et 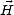 sont orthogonaux entre eux, la seulle composante non nulle de
sont orthogonaux entre eux, la seulle composante non nulle de 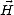 étant le
long de
étant le
long de 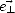 . De plus, d’après (B.21) et (A.10), les normes des champs électrique |
. De plus, d’après (B.21) et (A.10), les normes des champs électrique |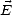 | et magnétique |
| et magnétique |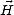 |
sont reliées par
|
sont reliées par
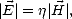 | (B.23) |
où 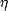 est l’impédance intrinsèque du milieu définie par
est l’impédance intrinsèque du milieu définie par
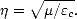 | (B.24) |