A multi-level approach for structural analysis with parallel architecture computers
Une Approche Multi-échelles pour des Calculs de Structures sur Ordinateurs à Architecture Parallèle
Résumé
Requirements for powerfull computers of numerical simulations lead to the development of new architectures, with distributed or shared memory, as well as the design of efficient algorithms that have to be suited to multiprocessor computers.
This work uses the Large Time Increment method (LATIN), in conjunction with a decomposition into substructures and interfaces. As efforts and displacements on interfaces are treated symmetrically, such an approach is a "mixed" one.
As a first step, we are concerned herein with the case of linear elasticity. Both choice and consequence of the discretisation of the unknowns are studied, especially when the treatment of efforts and displacements remains similar after discretisation.
The decomposition into substructures and interfaces conducts to define several scales for the problem. A multi-level extension is then built in order to take into account this particularity, and then to improve performance of the previous algorithm. This leads to the modification of the algorithm optimal parameter values, and of its interpretation. The proposed approach is then compared with other domain decomposition approaches.
The implementation within an industrial-like finite element code allowed us to validate this approach for examples with a large number of degrees of freedom, onto parallel computers with about 64 processors.
Le thème sous-jacent au travail de thèse est de réaliser des calculs implicites de structures, pour des chargements quasi-statiques et sous les hypothèses des petites perturbations, sur des ordinateurs à architecture parallèle. La méthode employée se classe dans la catégorie des méthodes de décomposition de domaine pour résoudre des problèmes de grande taille.
La méthode employée se propose de tirer parti du parallélisme intégré dans la Méthode A Grand Incrément de Temps (LATIN), proposée par Pierre Ladevèze et développée depuis plusieurs années au Laboratoire de Mécanique et Technologie de Cachan, couplée avec une méthode de décomposition de la structure en sous-structures et interfaces. Une première étude, restreinte au cas de l'élasticité plane, a permis de mettre en évidence que l'utilisation directe de cette approche, sans stratégie particulière, perd rapidement de son efficacité lorsque le nombre de sous-structures croît.
Le but du travail de thèse a été de montrer la faisabilité de l'intégration d'une stratégie multiéchelle (à 2 degrés de raffinement suivant une vision hiérarchique), pour pallier la difficulté précédente. L'adjonction d'un problème à grande échelle, global sur toute la structure, permet ainsi de prendre en compte les effets à grande longueur d'onde et de propager rapidement l'information parmi les sous-structures. Cette stratégie a été implantée dans le code de calcul de type industriel CASTEM2000 (maintenant Cast3M) de façon à pouvoir être portée sur différents calculateurs multiprocesseurs à mémoire distribuée. Un autre point clé est l'étude du choix des discrétisations des champs intervenant dans la méthode, pour ne pas complètement privilégier une approche en déplacement au détriment des quantités « statiques », en particulier pour les interactions entre les sous-structures et leur environnement, à savoir les interfaces qui leur sont connectées.
Fichier principal
 theseDureisseix.pdf (8.64 Mo)
Télécharger le fichier
theseDureisseix.pdf (8.64 Mo)
Télécharger le fichier
 annexe_ep_real.png (28.37 Ko)
Télécharger le fichier
annexe_ep_real.png (28.37 Ko)
Télécharger le fichier
 annexe_ep_mail_bw.png (10.25 Ko)
Télécharger le fichier
annexe_ep_mail_bw.png (10.25 Ko)
Télécharger le fichier
 annexe_roul_ecla2.png (4.87 Ko)
Télécharger le fichier
annexe_roul_ecla2.png (4.87 Ko)
Télécharger le fichier
 annexe_roul_mail2.png (55.16 Ko)
Télécharger le fichier
annexe_roul_mail2.png (55.16 Ko)
Télécharger le fichier
 annexe_roul_real2.png (29.24 Ko)
Télécharger le fichier
annexe_roul_real2.png (29.24 Ko)
Télécharger le fichier
| Format | Figure, Image |
|---|---|
| Commentaire | Rendu des 3/4 d'une éprouvette de traction multiaxiale |
| Format | Figure, Image |
|---|---|
| Commentaire | Maillage d'un seizième d'une éprouvette de traction multiaxiale (par raisons de symétries), utilisé pour tester une méthode de résolution numérique par sous-structuration. |
| Format | Figure, Image |
|---|---|
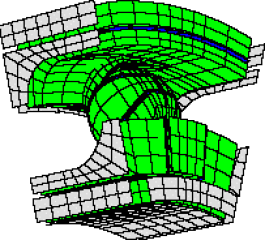
| Commentaire | Décomposition en sous-structures d'un secteur (périodicité géométrique) d'un roulement à billes à contact oblique. La simulation prend en compte les symétries de répétition. |
| Format | Figure, Image |
|---|---|
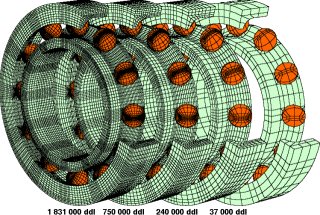
| Commentaire | Maillages éléments finis de tailles croissantes d'un roulement à billes. |
| Format | Figure, Image |
|---|---|
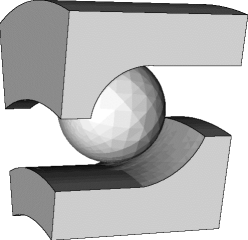
| Commentaire | Rendu d'un secteur (périodicité géométrique) d'un roulement à billes à contact oblique. |
Loading...
